La storia dei microprocessori

- L'automa di Alan Turing
- L'albegra booleana
- Variabili e costanti
- Il sistema binario
- Le tabelle di conversione del Sistema Binario
- Il bit
- Il byte
- I multipli del byte
- Le potenze a base 10
- Federico Faggin e la nascita del microprocessore
- La Very Large Scale Integration
- Diodi e transistor
- Il design del layer di una CPU
- La rifinitura dei dice
- I grandi produttori mondiali di CPU
- Il costo di produzione industriale delle CPU
- Il parallelismo di calcolo
- Il calcolo parallelo: esempio pratico
- I sistemi multi-core
- I 'System-on-a-Chip'
- La 'legge di Moore'
- La 'seconda legge di Moore'
Contattami velocemente
per richiedere una valutazione GRATUITA del tuo problema!
Network di computers per la difesa. Nuovi, potenti, allacciati a tutto, incaricati di dirigere tutto. Mi hanno detto che poi si sono evoluti. Un nuovo ordine d'intelligenza. E allora vedevano tutti gli uomini come una minaccia, e non solo quelli dell'altra parte. Decisero così il nostro fato in un microsecondo: sterminio.
Ormai tutta la nostra vita ne è completamente dipendente, e per qualsiasi processo risulta davvero difficile, se non impossibile, farne a meno.
Hanno cambiato il modo di produrre, lavorare e vivere di tutti gli esseri umani negli ultimi decenni, in maniera così dirompente e prepotente che il loro utilizzo di massa è stato definito la 'terza rivoluzione industriale'.
Costruiti dapprima enormi e poi più piccoli di una moneta da un centesimo, i processori di calcolo, chiamati anche CPU (Central Processing Unit) sono una delle conquiste più importanti di tutta la storia dell'umanità: hanno permesso di automatizzare flussi di lavoro prima impensabili, e hanno creato nuove potenzialità in settori saturi e depressi, mentre ne hanno creati tanti altri, in una fantastica epopea lunga decenni, in cui sono confluite le menti più geniali della storia: filosofi, matematici, ingegneri, fisici e scienziati vari; tutto e tutti per poter arrivare ad un piccolissimo chip capace di compiere milardi di operazioni al secondo.
Qui potrete trovare un breve riassunto di cosa è una CPU, da chi è stata ideata, come è realizzata e su quali basi lavora.
Buona lettura!
L'automa di Alan Turing

Alan Turing, il grande matematico inglese padre dell'informatica
Nel 1854, un uomo nomato George Boole pubblicò un libro particolare, che al tempo passò quasi del tutto inosservato: “An investigation of the laws of thought” ("Un esame sulle regole del pensiero").
Nessuno mai avrebbe detto che il libro sarebbe diventato in futuro un best-seller, e difatti all’epoca non lo comperò nessuno, lasciando il buon Boole povero in canna.
Nel libro vi era l’idea che tutto il pensiero umano, spogliato dalle sue verbosità e ridotto ai minimi termini (letteralmente) non era altro che un insieme sequenziale di scelte.
Secondo Boole, qualsiasi processo logico può essere ricondotto ad una sequenza di eventi elementari, non ambigui e dalla sintassi definita: tutto ciò prende il nome di algoritmo.

George Boole, che per primo definì i concetti di 'variabile' e 'costante' applicati al calcolo algebrico
Tutta l’informatica per come noi la conosciamo si regge su questa parola: un qualsiasi calcolatore non può comprendere la complessa sintassi di una qualsiasi delle lingue umane, ma lavora molto bene con il valore di certe costanti associate ad ogni singola variabile, e tutte questo può essere inserito in un algoritmo.
Questa interessante teoria fu ripresa, quasi un secolo dopo, da un altro matematico inglese, Alan Turing.
Turing ideò nel 1932 il primo famoso automa della storia, capace di eseguire calcoli complessi di natura algebrica: era la famigerata “macchina di Turing”.
L'automa di Turing è la sintesi della sintesi: un dispositivo dove registrare e richiamare informazioni (memoria) e un dispositivo di richiamo, lettura e modifica delle stesse (processore di calcolo). praticamente, per elaborare qualsiasi algoritmo non serve null’altro.
Turing non costruì mai un prototipo fisico del suo automa, anche perché a lui non interessava la parte squisitamente ingegneristica della faccenda, bensì quella puramente logico-matematica: se la macchina funzionava a livello prettamente logico, la sua dimostrazione reale era superflua.
A livello matematico, l'automa è una macchina in grado di risolvere calcoli complessi, e siccome determina sempre un risultato (qualsiasi esso sia) è di natura deterministica.
Che ci crediate o no, tuttora i calcolatori moderni non son altro che delle copie totalmente elettroniche della creazione di Turing.
Alan Turing non era solo un grande matematico e logico: era anche un campione di scacchi, parlava sette lingue fluentemente e un ottimo maratoneta.
Purtroppo, ebbe la sfortuna di dichiarare la sua omosessualità in un periodo storico non certo aperto mentalmente e culturalmente, e questo lo portò ad una serie impressionante di umiliazioni e sofferenze, concluse poi con il suicidio.
L'albegra booleana
Si chiama 'algebra booleana' quella parte dell'algebra che ha percepito il concetto espresso da George Boole (da cui il nome, per l'appunto) e che usa, per le sue operazioni, elementi ridotti ai minimi termini: variabili e costanti.
Viene correntemente usata come sistema per calcolare algoritmi, ed è - in estrema sintesi - un susseguirsi coerente e razionale di scelte.
Facciamo un esempio semplice: supponiamo che ora qualcuno vi debba chiedere di alzarvi ed uscire dalla stanza in cui siete.
Come si può descrivere questa richiesta con un linguaggio chiaro e non ambiguo?
Per esempio, così:
- Alzatevi (e passate al punto 2):
1.1- se siete seduti;
1.2 - se non lo siete, eseguite il comando e passate al punto 2; - Camminate verso la porta, (e passate al punto 3);
- Aprite la porta (e passate al punto 4)
3.1 - se non è già aperta;
3.2 - se già aperta, eseguite il comando e passate al punto 4; - Attraversate la porta, uscite dall’aula (e passate al punto 5);
- Avete finito (non fate nulla):
5.1 - se vi trovate fuori dall’aula;
5.2 - se non vi trovate fuori dall’aula,tornate indietro al punto 4.
Questo è un semplice esempio di algoritmo.
Volendo, si può usare qualcosa di più complesso.
Ecco un altro esempio: immaginiamo di dover uscire con una ragazza che però non conosciamo fisicamente, ma diciamo che è una conoscenza di famiglia e perciò ci toccherebbe uscire.
Ora, della ragazza ignoriamo tutto, ed effettivamente non sappiamo se vogliamo effettivamente andare all’incontro oppure no.
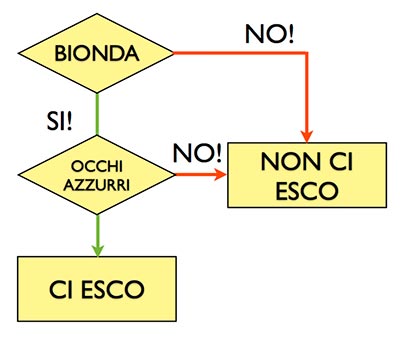
Dediciamo quindi che, a nostro gusto, usciremo con la ragazza se e solo se sarà bionda e con gli occhi azzurri.
Se anche solo una delle due variabili non sarà soddisfatta, non usciremo con la ragazza.

Quindi, ricapitolando: usciamo con la ragazza se e solo se:
- È bionda;
- Ha gli occhi azzurri
In caso contrario,tutte le altre combinazioni saranno invariabilmente cestinate, e noi non usciremo con la ragazza.
Per cui, schematizzando, possiamo tracciare due diagrammi di flusso per analizzare la situazione, e useremo due simboli grafici standard per dare sostanza al tutto:
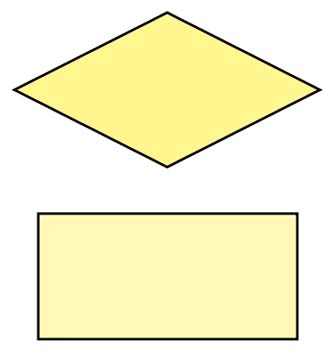
Controlleremo le opzioni del diagramma con il rombo, menre per le decisioni useremo il rettangolo.
Nei rombi vediamo le opzioni, che ad onor del vero possono variare e quindi le chiamiamo variabili, e vediamo pure le decisioni possibili.
Avremo esito positivo se e solo se la ragazza avrà i capelli biondi e gli occhi azzurri: se anche solo una delle due opzioni non è soddisfatta, avremo esito negativo.
Tutto ciò è chiaro e non ambiguo, quindi può essere usato per costruire un algoritmo.
Ma se volessimo essere meno pignoli e ci accontentassimo pure di una sola delle due caratteristiche richieste?
Riformulando col nuovo criterio, usciremo con la ragazza se ha almeno una di queste caratteristiche:
- È bionda;
- Ha gli occhi azzurri
In questo caso, questo risulta essere il nostro diagramma:
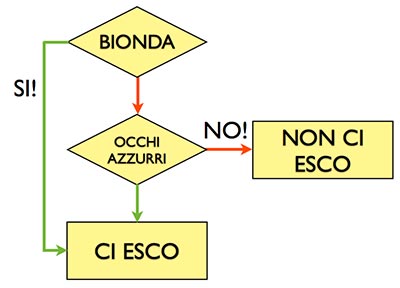
Vediamo le decisioni possibili: avremo esito positivo se la ragazza avrà i capelli biondi oppure occhi azzurri; avremo esito negativo se invece nessuna delle due opzioni è soddisfatta.
Ecco riproposti i diagrammi per la comparazione:
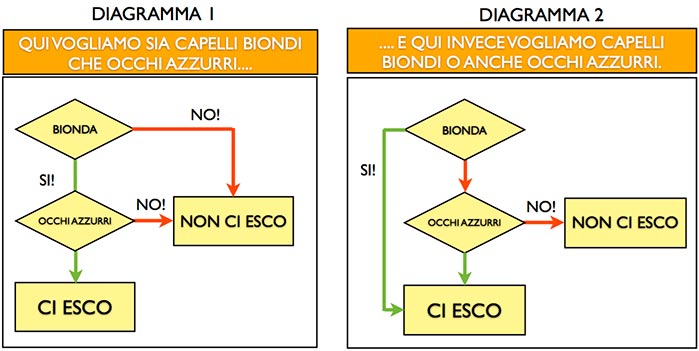
Notiamo subito come i due diagrammi, seppur con le stesse variabili e decisioni finali, sono profondamente diversi: il primo non è tollerante e vuole soddisfatte tutte e due le variabili, mentre il secondo ci va un pelo più leggero e si accontenta di una sola delle due.
Tutto ciò ha senso nel calcolatore biologico di un essere umano (il cervello), ma le cose si fanno ben più complicate quando dobbiamo istruire una macchina che non può capire il nostro complesso pensiero.
Dobbiamo quindi convertire nomi, verbi e regole grammaticali varie in costanti e variabili che un calcolatore, per esempio un automa di Turing, può capire.
Per fare ciò, ci viene in aiuto George Boole con la sua algebra booleana.
Variabili e costanti
Vediamo la seguente tabella:
| OPERAZIONE | ISTRUZIONE | OPERATORE |
|---|---|---|
| Controllo | IF (se) | |
| Azione | THEN (allora) | |
| Congiunzione | AND (e) | AND |
| Separazione | OR (oppure) | OR |
| Negazione | NOT (no, non) | NOT |
Proviamo ora ad assegnare delle generiche lettere alle variabili del nostro esempio della ragazza visto in precedenza, e per specificare meglio, diciamo subito che un evento può essere variabile, mentre invece un’istruzione booleana è costante:
a = capelli biondi; b = occhi azzurri; c = ci esco
; x = capelli non biondi; y = occhi non azzurri; z = non ci esco
Tenendo sempre a mente di usare le istruzioni della tabella, tentiamo di risolvere in maniera logica i due diagrammi visti in precedenza.
Andiamo quindi a vedere cosa si può combinare con il diagramma 1: secondo esso, per uscire con la ragazza bisogna riscontrare entrambe le variabili in esame.
Quindi possiamo scrivere che:
IF a AND b THEN c
Tradotto in lingua comprensibile, seguendo le istruzioni in tabella se ne desume che:
SE capelli biondi E occhi azzurri ALLORA ci esco
Quindi, come già sappiamo usciremo con la ragazza se e solo se entrambi gli eventi sono positivi.
Ne desumiamo dunque che:
IF a AND y THEN z
Poichè una delle variabili è negativa, il risultato è a sua volta negativo, e non combacia con i nostri voleri.
In lingua più comprensibile avremo:
SE capelli biondi E occhi non azzurri THEN non ci esco 18
Ma c’è rimasto un altro esempio da vedere, e per quanto ovvio va comunque menzionato:
IF x AND y THEN z
Che ovviamente tradotto risulta come:
SE capelli non biondi E occhi non azzurri ALLORA non ci esco
Quindi, da ciò abbiam capito che l’operatore AND elabora sempre un risultato positivo se e solo se tutte le variabili sono soddisfatte (positive).
Se anche una delle variabili non è soddisfatta positivamente, AND elabora sempre un risultato negativo.
Per noi esseri umani è facile da intendere, ma come farlo capire ad un calcolatore che invece può elaborare solo mero codice binario, quindi in pratica solo due variabili?
Analizziamo di nuovo la conversione delle variabili in lettere:
a = capelli biondi; b = occhi azzurri; c = ci esco; x = capelli non biondi; y = occhi non azzurri; z = non ci esco
Risulta subito evidente che, forse, sei variabili distinte poi non servono a tanto.
Sì, perché tanto a, b e c hanno comunque valenza positiva, mentre x y e z negano sempre un qualcosa.
Se applichiamo allora i due numeri del codice binario 1 e 0 ai due gruppi di variabili?
Facciamolo, e definiamo pure per convenzione 1 come variabile sempre positiva (che possiamo definire vera) e 0 come variabile sempre negativa (che possiamo definire falsa).
Detto ció, proviamo a riscrivere le nostre equazioni.
La precedente equazione:
IF a AND b THEN c
Riscritta secondo la nuova convenzione diventa:
IF 1 AND 1 THEN 1
Che volendo si puó ancora di più semplificare in:
1 AND 1=1
Ma abbiamo detto che la variabile 1 può anche significare vero: 'true' in lingua inglese.
Perciò:
1 AND 1=TRUE
E per le specifiche proprietà dell’operatore and di cui abbiamo parlato in precedenza, ne consegue che:
1 AND 0=0
Dove il risultato 0 può anche essere inteso come falso: 'false', sempre in lingua anglofona:
1 AND 0=FALSE
E questa è algebra booleana.
Con soli due numeri e tre operatori il calcolatore può calcolare di tutto.
Però abbiamo visto solo un operatore, AND: cosa accade con gli altri due operatori?
Vediamo ora in dettaglio le loro proprietà.
L’operatore OR (oppure), come suggerisce il nome, elabora un risultato positivo (TRUE) se e solo se una delle variabili è vera (TRUE).
In caso contrario, restituisce un risultato negativo (FALSE).
1 OR 0=TRUE
0 OR 1=TRUE
1 OR 1=TRUE
0 OR 0=FALSE
E per ultimo abbiamo l’operatore NOT che inverte la variabile di ingresso:
1 NOT 0=FALSE
0 NOT 1=TRUE
Per tenere bene a mente le proprietà dei singoli operatori booleani, è utile seguire queste semplici tabelle, chiamate tavole di veridicità:
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| A | B |
|---|---|
| 1 | 0 |
| 0 | 1 |
Tutto ciò come si integra con il flusso elettronico di un processore?
Vediamolo.
Teniamo a mente che il numero binario 1 può essere associato sempre a cose positive, come ad esempio un segnale elettrico; mentre il numero binario 0 si associa bene a cose negative, come l’assenza di un segnale elettrico.
Esaminiamo questo semplicissimo circuito, collegato ad una batteria che accende una lampadina:
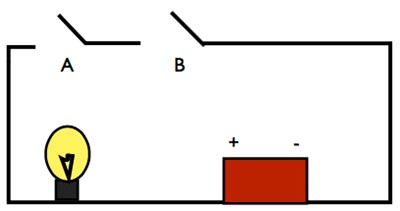
Se lo compariamo con la tabella dell’operatore AND, vediamo che se gli interruttori A e B son abbassati (quindi abbiamo una variabile C=1, quindi TRUE), il circuito si chiude e la lampadina si accenderà.
Immaginate questo circuito in piccolo, molto più piccolo: piccolo quanto basta da essere presente a milioni in un chip di pochi micron.
State già immaginando cosa pulsa nel cuore di un microprocessore, o meglio: di un’unità logico-matematica dello stesso.
Come l’operatore AND ha il suo ruolo in un circuito, così anche gli operatori OR e NOT svolgono il loro lavoro tutti insieme per costruire altri circuiti di altre porte logiche.
Con solo due numeri, tre operatori ed altrettanti circuiti, si possono eseguire un numero infinito di calcoli.
Vediamo gli schemi elettrici degli altri due operatori:
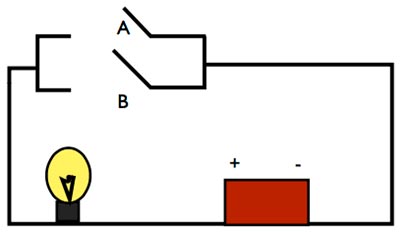
Questo è l’esempio di un circuito corrispondente all’operatore OR.
Come è facile intuire, la lampadina si accenderà se almeno una delle variabili nella tabella OR sia TRUE.
Non ci rimane che un ultimo operatore da vedere, ovvero NOT:
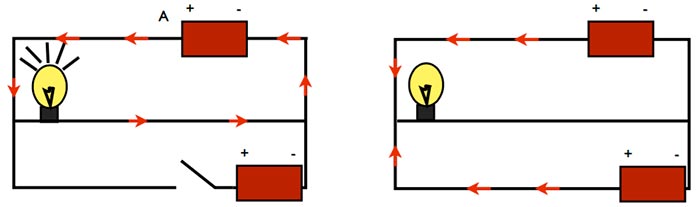
Come si può vedere, quando l’interruttore è aperto (A=FALSE), solo una batteria alimenta il circuito e la lampadina è accesa.
Ma quando a è TRUE, l’interruttore mette in circuito anche la seconda batteria, che fa fornisce corrente eguale ed opposta, impedendo alla lampadina di accendersi.
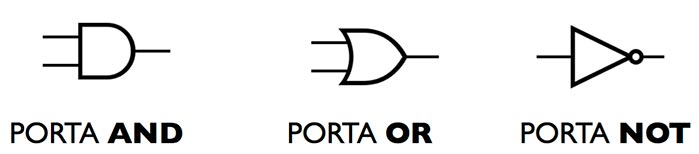
Tutti questi circuiti, che in un processore sono presenti a milioni grazie alla miniaturizzazione dei loro componenti, sono chiamati porte logiche, e possono essere rappresentati anche con simboli standard:
Ovviamente,tutte e tre le porte possono essere combinate tra di loro per adattare qualsiasi algoritmo.
Ecco infatti come un processore tratta il nostro esempio della ragazza, nel diagramma 2 (ci usciamo sia con occhi blu che con capelli biondi):
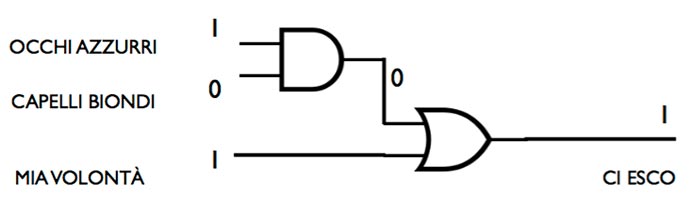
Grazie all’operatore OR, il calcolatore ora può elaborare in senso non ambiguo la sottile differenza con il diagramma 1, e fornire quindi un output idoneo.
Sebbene con sole tre porte logiche si possano eseguire tutti gli algoritmi immaginabili, per comodità gli ingegneri elettronici tendono a costruire porte logiche accorpate, oppure porte logiche “inverse” (si dice negate) alle tre basilari: si risparmia in spazio e si guadagna in snellezza di progettazione, e di conseguenza in esborso economico.
Ci sono quindi le porte logiche NOR, XOR, NAND e XNOR.
Le porte logiche sono costruite fisicamente grazie a diodi e transistor, e sfruttano tutte un determinato effetto fisico proprio dei semiconduttori al silicio, chiamato giunzione P-N.
Le moderne CPU possono contenere miliardi di transistor e diodi in un piccolissimo chip di pochi millimetri di lato, oltreché svariate unità logico-matematiche che lavorano in parallelo, rendendo quindi più veloce la computazione.
Il sistema binario

Gottfried Leibniz, l'inventore del sistema numerico binario
Verso la fine del 1600, il grande scienziato e filosofo tedesco Gottfried Leibniz inventò un sistema di rappresentazione numerica sbalorditivo per lʼepoca, poiché basato solo sullʼutilizzo di due simboli, per convenzione 1 e 0.
Sebbene a prima vista non intuitivo, il metodo di Leibniz fu concettualmente rivoluzionario, poiché grazie a soli due simboli era possibile ottenere un numero infinito di combinazioni derivate.
A ben vedere, lʼinnovativo sistema numerico poi tanto complicato a livello concettuale non era, poiché risultava nondimeno che un sistema posizionale a base 2, e questo lo rendeva differente dal sistema numerico a base 10 che allora come ora tutti usavano.
Il sistema numerico a base 10, essendo molto più comodo per un essere umano (principalmente per via dei nostri primi rudimentali calcolatori, le dita) non permise all'intuizione di Leibniz di prendere piede tra la gente, e pertanto il suo sistema numerico binario non ebbe mai successo come nuovo standard e cadde nel più completo dimenticatoio per quasi due secoli, almeno sino a che Alan Turing non lo rispolverò ad hoc per l'ideazione del suo automa.
Le tabelle di conversione del Sistema Binario
Essenzialmente, il sistema numerico binario fa quel che promette, ovvero risolvere la rappresentazione di qualsivoglia numero naturale con solo due valori, lo 0 e lʼ1.
Come lo fa, è materia molto semplice: Leibniz intuì già due secoli prima lʼimportanza della sintesi tanto cara a Boole, ed è proprio in questo concetto di semplificazione assoluta che il sistema binario trova la sua forza e la sua ragion dʼessere.
Come in tutti i sistemi di rappresentazione (non solo numerica) il sistema binario associa a simboli particolari significati particolari, con una logica ben precisa.
Ovviamente, essendo in base 2, tutti i numeri rappresentati con questo sistema sono per forza di cose 1, 0 o combinazioni delle due variabili.
Vediamo qui sotto una semplice tabella di conversione da sistema numerico in base 10 a sistema numerico binario in base 2 dei numeri naturali da 0 a 10:
| SISTEMA NUMERICO A BASE 10 | SISTEMA BINARIO |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
Come risulta ben chiaro dalla tabella, le variabili 0 ed 1 seguono una logica ben precisa per rappresentare i numeri in base 10.
Infatti, prima di aggiungere una variabile al numero da rappresentare, tutte le possibili combinazioni numeriche devono essere esaurite.
Così, se con solo una variabile si può rappresentare solo 0 od 1, con due variabili si possono rappresentare i numeri naturali 2 o 3.
Per rappresentare il numero naturale 4, per forza di cose bisogna aggiungere una variabile: si parte sempre dallo 0 e via via si va a riempire le combinazioni possibili sino a che non si finisce con tutti 1.
Con tre variabili, possiamo rappresentare quattro numeri naturali; con cinque variabili, otto.
Con sei variabili, sedici numeri, e via via, si va sempre al raddoppio delle possibilità di rappresentazione. La regola si può ripetere allʼinfinito, visto che i numeri sono infiniti.
Se per il pensiero umano con questo sistema risulta difficile rappresentare numeri e farne di conto (come detto ci troviamo molto meglio con base 10), tutto ciò risulta perfetto per l'unità logico-matematica di un calcolatore elettronico (l'ALU), che è formata da porte logiche che a loro volta risolvono algoritmi per mezzo di equazioni booleane, che pretendono e necessitano solo di due variabili per svolgere il loro lavoro alla perfezione.
Dopo quasi duecento anni quindi, il geniale sistema di rappresentazione ideato da Leibniz trovò la sua giusta collocazione nella storia umana: diventò la base fondamentale per quella che è stata ribattezzata da molti la “terza rivoluzione industriale”, ovvero lʼinformatica su computazione elettronica.
Il bit
Alla luce del sistema binario appena analizzato e ricordandoci sempre dellʼalgebra booleana e delle sue variabili, cosa sta esattamente a significare la parola bit?
Effettivamente, il bit può significare due cose interconnesse è vero, ma estremamente diverse:
- Può significare 'binary digit', quindi numero binario.
Altro non è che 0 od 1, ovverosia una delle due rappresentazioni numeriche possibili del sistema binario. In questo contesto, con il calcolo elettronico il bit può anche non entrarci per nulla, è solo un simbolo di rappresentazione di un sistema numerico; - Può significare 'binary unit', ed in questo caso il suo contesto cambia radicalmente, perché assume il significato di unità minima di informazione del calcolo elettronico.
Lo 0 e lʼ1 rappresentano due variabili booleane, che trattate con le relative costanti (operatori), servono alle porte logiche per rendere possibile il calcolo elettronico.
La differenza, come vedete, non è per nulla sottile: mentre il binary digit è solo un numero di un sistema di rappresentazione, il binary unit è lʼunità minima di informazione che una porta logica di una ALU riesce a “comprendere” e trattare con dovizia.
In entrambi i casi, comunque, il bit può essere inteso indifferentemente come 0 ovvero 1.
Nel Sistema Internazionale dei Pesi e delle Misure, il bit è sempre scritto minuscolo, ed è importante tenerlo a mente.
Il byte
In informatica, che sia 0 od 1 il bit rappresenta due variabili di eguale importanza, ed anche di eguale probabilità di esecuzione.
Le porte logiche distinguono la differenza tra 0 ed 1 grazie alla tensione elettrica: se la tensione cala oltre un certo voltaggio, il segnale sarà una variabile 0.
In caso contrario, sarà 1.
È quindi del tutto inesatta la comune credenza che 1 e 0 vogliano significare 'passaggio di corrente' invece di 'niente passaggio di corrente'.
In una macchina perfetta (teorica) sì, lʼaccezione corrisponderebbe al vero, ma nel processo di costruzione delle porte logiche (e, soprattutto, nellʼeffetto transistor) nella pratica costruttiva questo è irrealizzabile. Però, come ci dice il sistema binario, con un solo bit in realtà possiamo rappresentare veramente pochi valori, per lʼappunto solo due.
Solo due valori sono un poʼ pochino per far di conto seriamente (non credo sia mai esistita una CPU con registri a due bit), quindi sin dagli albori dellʼinformatica il bit è stato moltiplicato, per ottenere più rappresentazioni numeriche e, di conseguenza, calcoli che risolvano algoritmi più o meno complessi.
Se nei registri di una CPU la word ci da la dimensione massima di informazioni (quindi bit) che lʼALU riesce a elaborare singolarmente, la dimensione minima di dati ed istruzioni che la CPU “morde” dalla memoria principale con un solo indirizzo logico è chiamata byte: non a caso è stata usata la colorita espressione "morde", infatti il verbo rende bene lʼidea, ed anche la parola byte nella lingua inglese suona uguale al verbo bite, ovvero mordere.
Quindi, possiamo ben affermare che il byte è lʼunità fondamentale della misura della memoria, nella computazione elettronica.
La quantità di bit in un byte non è stata sempre uguale ed è cambiata nel corso degli anni, soprattutto grazie a CPU sempre più potenti in elaborazione grazie alle nuove tecnologie di costruzione.
Allo stato attuale delle cose, benché non sia unʼunità di misurazione standard, si considera un byte formato da otto bit.
Molti programmatori ed ingegneri (soprattutto europei) chiamano il byte con il più corretto nome di ottetto, e tale parola risulta molto più chiara quando si deve ad esempio riferirsi ad architetture passate in cui il byte era inferiore agli otto bit attuali.
Ragionando in sistema binario a base 2, se un bit può essere 1 o 0 (quindi due valori) e il byte sono otto bit, vien subito da pensare che:
28=256
Quest'elevazione a potenza in base 2 è il succo di tutta lʼinformatica su computazione elettronica: come già accennato infatti, avendo solo due valori con cui far di conto le porte logiche delle ALU elevano numeri elevati con potenze a base 2.
Quindi, invece che moltiplicare il numero 2 per otto volte, si usano le più comode (ed in questo caso obbligate) potenze.
Perché oggi si usano byte da otto bit, che danno 256 possibili valori?
Cʼè un motivo preciso o è solo per qualche convenienza particolare?
Effettivamente, entrambe le cose.
Lungo sarebbe il discorso, ma si può sintetizzare brevemente con una piccola serie di constatazioni:
- Per ingannare lʼocchio umano con una sfumatura uniforme dal bianco al nero, occorrono circa 200 toni di grigio;
- Per riprodurre il testo di una qualsiasi lingua occidentale, occorrono più di 200 caratteri (compresi quelli accentati);
- Servono più di 200 livelli dʼintensità per riprodurre un suono abbastanza fedele
Questa breve lista può darvi unʼidea abbastanza chiara del perché di un byte ad otto bit, che comunque non sono ancora sufficienti per memorizzare tutte le grandi quantità di dati che al giorno dʼoggi tutti noi usiamo.
Ad onor del vero, otto bit non erano sufficienti nemmeno vent'anni fa per scrivere un banalissimo file di solo testo.
I multipli del byte
Per ovviare al problema della carenza di bit per memorizzare informazioni, il byte si moltiplica, proprio come i multipli del Sistema Internazionale che conosciamo sin da piccoli.
Anche i nomi dei multipli son gli stessi, e vengono sempre dallʼantico greco.
Prima di partire con la tabella dei multipli, è bene sottolineare che il simbolo standard del byte, dettato dalla Commissione Elettrotecnica Internazionale è il B; effettivamente, la lettera maiuscola è storicamente riservata alle unità di misura tratte dai cognomi degli inventori, ma in questo caso si è deciso di fare unʼeccezione per via della cattiva abitudine di molti nellʼindicare il bit solo come b (sbagliatissimo), con conseguente logica confusione.
Confusione che come vedremo, per forti interessi commerciali si è comunque creata.
Andiamo con ordine ed analizziamo tabella dei multipli del byte presente qui dabbasso.
Ricordiamoci sempre, e questo è importante, che tutti i multipli sono potenze a base 2:
| NOME | SIMBOLO SI | MULTIPLO |
|---|---|---|
| kibibyte | KiB | 210 |
| mebibyte | MiB | 220 |
| bigibyte | GiB | 230 |
| tebibyte | TiB | 240 |
| pebibyte | PiB | 250 |
| exbibyte | EiB | 260 |
| zebibyte | ZiB | 270 |
| yobibyte | YiB | 280 |
Questi sono i multipli del byte calcolati con potenze in base 2, ed a ogni passaggio di multiplo lʼesponente aumenta di 10 unità: al calcolo elettronico non serve altro per operare al meglio.
Però, sicuramente a molti di voi nomi dei prefissi come kibi, mebi e gibi risulteranno un poco strani, e magari invece qualcosa come kilo, mega e giga sarebbe risultata più familiare.
Perché questa cosa?
La risoluzione al dilemma ha generato e genera tanta, troppa confusione, non solo tra la gente comune, ma incredibilmente anche tra molta gente che con lʼinformatica ci lavora seriamente.
Vedremo ora da che cosa è generata tutta questa confusione sui nomi dei multipli del byte.
Le potenze a base 10
Agli albori dellʼinformatica, quando le capacità di memorizzazione delle memorie erano veramente esigue e la potenza di calcolo di una CPU era modesta, era abbastanza diffusa lʼopinione che mai e poi mai in futuro si sarebbero superati i mille byte per la memorizzazione dei dati, anche considerando che allʼepoca un byte non era di otto bit ma di dimensione inferiore, variabile da costruttore a costruttore.
A questo, è sempre bene ricordare lʼatavica preferenza umana nel convertire il sistema di misurazione con potenze a base 10, che rende tutti i nostri calcoli mnemonici molto più semplici.
Per una curiosa coincidenza, un kibibyte è 210 (quindi 1.024 B), che è una cifra molto vicina a 1.000.
Considerando le nostre naturali attitudini ad elevare tutto con potenze di 10, vien subito da convertire 1.000 in 103.
Come ci hanno insegnato sin da piccoli, infatti, ogni multiplo di 10 infatti è semplice da convertire in potenza: conta gli zeri, hai lʼesponente.
Quindi, senza andar troppo per il sottile e complice anche il Sistema Internazionale ed i suoi multipli a base 10, alcuni ingegneri e programmatori per definire 1.000 byte hanno cominciato ad usare erroneamente potenze di 10 rispetto alle corrette potente di 2.
Se tutto ciò risulta molto comodo per un essere umano (ci si ricorda meglio la cifra tonda di 1.000 che di 1.024), è incompatibile con i calcoli binari di una CPU, che moltiplica bit su bit con potenze a base 2.
Questo errore voluto per semplificare le cose agli umani, genera nel calcolo a base binaria un errore del 2,4%, crescente.
Se un errore del 2.4% risulta più o meno accettabile per modeste quantità di byte, diventa veramente considerevole a multipli maggiori.
Vediamo quindi la tabella nella prossima pagina per renderci conto dei multipli del byte a base 10 con relativi margini di errore.
| NOME | SIMBOLO SI | MULTIPLO | PERCENTUALE ERRORE |
|---|---|---|---|
| kilobyte | KB | 103 | +2,4% |
| megabyte | MB | 106 | +4,9% |
| gigabyte | GB | 109 | +7,4% |
| terabyte | TB | 1012 | +10% |
| petabyte | PB | 1015 | +12,6% |
| exabyte | EB | 1018 | +15,3% |
| zettabyte | ZB | 1021 | +18% |
| yottabyte | YB | 1024 | +20,8% |
Come ben vediamo, i nomi ed i simboli del Sistema Internazionale fanno un poco a cazzotti con quelli della Commissione Elettrotecnica Internazionale, che invece da anni si sforza per far usare da tutti i nomi corretti che definiscono le corrette potenze a base 2.
Approvando senza remore le buone intenzioni della CEI, va però sottolineato che i nuovi nomi corretti non sono mai entrati nellʼuso comune, e bisogna pure dire che anche molti Sistemi Operativi attualmente in uso (anche quelli più diffusi), sebbene calcolino i multipli del byte con potenze a base 2, mostrano comunque allʼutente i simboli del Sistema Internazionale, ormai entrati nel gergo comune.
Tutto ciò genera da anni una grande confusione, e come sempre accade in questi casi tra i due litiganti (Sistema Internazionale e Commissione Elettrotecnica Internazionale) il terzo se la gode: infatti i produttori mondiali delle memorie utilizzano, per propaganda, i simboli del Sistema Internazionale con multipli a base 10 (correttissimi, legalmente parlando), mentre tutti i calcolatori esistenti al mondo memorizzano byte con potenze a base 2.
Questo porta ad una riduzione della capacità effettiva di stoccaggio secondo la percentuale di errore riportata in tabella.
Ora come ora, dopo decenni di bombardamento scorretto, risulta davvero difficile usare i nuovi prefissi della CEI: va anche detto che i nomi sono davvero assurdi, ed alcuni fanno proprio ridere (gibibyte e tebibyte son terribili a pronunziarsi e sentirsi).
In generale, tutti usano ancora i prefissi SI ed i loro relativi nomi, e possiamo farlo anche noi, essendo però consapevoli che stiamo lavorando sempre a potenze in base 2.
Federico Faggin e la nascita del microprocessore

Federico Faggin, il padre del microprocessore e della tecnologia 'silicon gate'
Sul finire degli anni '60 del 1900, un giovane ingegnere italiano chiamato Federico Faggin, all'epoca impiegato dell'Intel, cominciò a mettere a punto un processo tecnologico innovativo basato sui semiconduttori al silicio, che chiamò 'silicon gate'.
Tale processo aveva obiettivi importanti: raggruppare tutti i componenti logici di una CPU (ALU, Memory Management Unit, registri, cache, ecc ecc.) in un unico chip integrato, di dimensioni enormemente contenute e dal costo di produzione più basso rispetto ad una canonica - al tempo - unità di processo di calcolo.
Già nel 1958, John Hoerni della Fairchild Semiconductor aveva proposto la produzione di semiconduttori partendo direttamente da un blocco di silicio (wafer), ricavando poi transistor e diodi tramite un processo planare.
Faggin partì dal pioneristico lavoro di Jack Kilby della Texas instruments, che per primo riuscì a connettere due transistor ricavati dalla stessa fetta di silicio: si convinse che l'incisione planare era davvero la chiave di volta per costruire unità CPU con costi industriali molto più contenuti rispetto alla produzione di allora, e virò completamente verso la tecnologia MOS (metallo-ossido-conduttore) recentemente sviluppata per la costruzione di nuovi transistor.

L'Intel 4004, il primo microprocessore della storia
Dopo anni di ricerche e sperimentazioni, nel 1971 Faggin riuscì a ricavare tutti i componenti di una CPU in un singolo, piccolissimo chip: era il famoso Intel 4004, il primo microprocessore della storia.
Il processo che portò alla costruzione del primo prototipo funzionante fu migliorato costantemente da Faggin, e venne chiamato "Large Scale Integration", evolutosi poi in "Very Large Scale Integration".
Grazie al lavoro di Faggin, a cui la Intel deve tutta la sua fortuna, si poterono cominciare a costruire microprocessori potenti e a basso costo, aprendo la strada alla terza rivoluzione industriale.
Con word da 8 bit, 16 registri da 8 bit e 2.300 transistor incisi tramite serigrafia su un unico blocco monolitico in silicio, l'Intel 4004 non sono era il primo microprocessore della storia, ma era anche una CPU estremamente evoluta per l'epoca: poteva controllare anche il bus della memoria e quello dell'input/output, e la sua frequenza di clock era di circa cinque volte superiore a quella di una paritaria CPU dell'epoca, costruita non monoliticamente e con differente tecnologia.
Non di meno, lo spazio occupato dal die era di circa la metà rispetto ad un equivalente con tecnologia al germanio.
La Very Large Scale Integration

Un wafer con i dice già pronti per il ritaglio
Lo sviluppo dell'Intel 4004 di Faggin aprì le porte ad un nuovo sistema di produzione dei semiconduttori al silicio, dallo stesso ingegnere italiano progettato e chiamato 'silicon gate'.
Grazie a questo processo, è possibile ridurre la dimensione di diodi e transistor in maniera considerevole, tanto da riuscirne ad infilare a milioni in un singolo, piccolissimo circuito integrato, costruendo quindi una CPU monoblocco.
Tutto il procedimento è effettuato a ciclo continuo, partendo da un unico blocco di silicio puro, ottenuto tramite il processo Czochralski: per mezzo della naturale aggregazione dei cristalli - che tendono sempre a disporsi su strutture tridimensionali ben definite - l'industria riesce ad ottenere cilindri di silicio puro, che vengono poi tagliati a mo' di pizza, ottenendo lastre circolari perfette chiamate wafer.
Lo spessore di un wafer varia a seconda delle fasi della lavorazione, ma in generale si taglia inizialmente a 0,5 mm: a wafer completamente lavorato lo spessore sarà di pochi micron.
Dopo il taglio (con particolari seghe industriali al diamante, oppure con seghe laser), il wafer viene lavato, smussato al bordo e piallato per rendere le due facce perfettamente parallele (ciò è essenziale per il buon funzionamento del prodotto finale).
L'effetto tunnel è quel fenomeno fisico quantistico che permette il funzionamento dei diodi e dei transistor, rendendo di fatto possibile la computazione elettronica per come noi la conosciamo.
Per la famosa legge di conservazione dell'energia (da cui deriva il primo principio della termodinamica) è impossibile che un dato sistema isolato possa passare energia ad un altro sistema isolato di energia superiore.
In altre parole: la trasmissione d'energia corre sempre a senso unico, da dove è presente in quantità maggiore a dove è invece presente in quantità minore.
Ovviamente, per 'sistema isolato' si intendono sistemi unitari complessi (ad esempio: il motore a combustione interna di una generica vettura) oppure unitari, come ad esempio le particelle subatomiche.
Questo è un principio fondamentale della meccanica classica, e per quanto ne sappiamo al momento è vero, tanto da essere chiamato da alcuni 'legge'.
Nel mondo dell'immensamente piccolo, però, succede un fenomeno curioso: alcune particelle, se messe in particolari condizioni, riescono a sfuggire a questa legge, e riescono pertanto a 'superare' una determinata barriera che ha energia totale maggiore della loro.
Questo effetto, che può essere spiegato solo in un campo quanto-meccanico, è chiamato 'effetto tunnel', ed è quello che accade costantemente ai diodi e ai transistor presenti in ogni CPU costruita fino ad ora: quando lo strato di ossido che separa la parte positiva da quella negativa si assottiglia fino ad un piccolissimo spessore (parliamo di dimensioni nano), alcuni elettroni riescono comuque a 'bucare' la zona di svuotamento, e permettere così la conduttanza elettrica.
Il fenomeno è accertato ed osservato ormai da quasi un secolo, da quando il grande fisico austriaco Erwin Schroedinger stilò la fondamentale equazione che porta il suo nome, dimostrando che i sistemi evolvono di stato nel tempo, più o meno con la funzione di un'onda.
Per farla più semplice di quello che è, l'onda degli elettroni in un effetto tunnel non s'abbassa mai a zero, anche quando s'infrange contro una barriera apparentemente insormontabile come quella dell'ossido presente nei transistori: ne consegue che una discreta quantità d'elettroni riesca ad infrangere le leggi della meccanica classica, e a passare da uno stato di bassa energia ad uno stato di energia superiore.
Del perché questo accada, al momento non abbiamo spiegazioni plausibili, e pertanto dobbiamo semplicemente accettarlo, in attesa di trovare una motivazione coerente con il nostro modello standard (oppure, attendere un nuovo modello).
L'effetto tunnel è ampiamente usato nei transistori MOSFET, che vengono incorporati a livello nanoscopico nelle attuali CPU e memorie a stato solido.
A seconda dei processi produttivi, durante il piallamento il wafer può già subire drogaggio o meno: nel caso, il drogaggio per caratterizzarne la conduttività elettrica è solitamente fatto o con gasatura (il wafer viene cotto ad elevate temperature con gas ionizzanti, di solito azoto o argon), oppure per instillazione ionica (molto più precisa ma anche molto più costosa).
Il drogaggio è quel procedimento grazie al quale si modifica in parte la composizione elettrica del materiale, creando zone a differente induttanza elettrica, sia positiva che negativa.
Il materiale originale però rimane elettricamente neutro, in quanto le nuove zone create si compensano tra di loro, essendo eguali in quantità; il drogaggio risulta indispensabile per creare diodi e transistor, e farlo direttamente prima della lavorazione del wafer fa risparmiare molto tempo di lavorazione.
Finita questa prima preparazione, il wafer è pronto per essere più propriamente lavorato per farne il supporto di circuiti integrati.
Solitamente (ma il processo cambia da industria ad industria e da esigenza ad esigenza), il wafer viene inciso a strati, con tutti i circuiti integrati delle sue CPU, che in gergo tecnico vengono chiamati layer.
Diodi e transistor
A seconda del tipo di drogaggio del wafer, anche i layer possono essere più o meno ionizzati, dimodo da formare microscopici diodi e transistori.
Per far questo si utilizza una particolare deviazione della litografia, stavolta applicata a maschere di incisione davvero microscopiche (stiamo sempre nellʼordine dei nanometri).
Per completare una moderna CPU, spesso si devono stratificare 20 o più layer, in un processo molto lungo, che di solito dura quasi due mesi di lavorazione ininterrotta.

Il wire bonding è il processo di connessione della CPU ai contatti elettrici (pin) del package
Tutto è molto costoso, anche perché ogni layer viene inciso sul wafer singolarmente, e non può essere riutilizzato.
In più, le lastre sono costruite di solito in cromo o quarzo ed incise con cannoni laser od a elettroni, strumenti ad altissima precisione ma dal costo proibitivo (un singolo cannone laser del genere può costare sino a 10 milioni di dollari).
Il design del layer di una CPU
Ogni modifica al design del layer comporta anche un necessario aggiornamento di tutti gli altri layer collegati, da qui il motivo per cui l'industria tende sempre a sfruttare processori divenuti non più così performanti per scopi di ri-utilizzo, come ad esempio sistemi embedded.
Tramite la litografia e particolari lampade ad elettroni e raggi UVA, lo schema dei layer viene fissato sul wafer, che poi è pronto a ricevere il passaggio fondamentale di itching, ovvero la microincisione dei circuiti.
Questa può essere fatta in vari modi, tramite laser o per aggressione acida.
Ovviamente, ogni layer comporta un passaggio di litografia ed uno di incisione, da cui la grande quantità di tempo-lavoro per completare un wafer ed estrarne i singoli chip.
Tra unʼincisione di un layer ed unʼaltra, il wafer viene anche piallato e parallelizzato, per cui altro tempo- lavoro.

La rifinitura dei dice
Dopo circa 20 layer applicati, il wafer con tutti i suoi chip (vengono anche chiamati dice, ovvero dadi) è pronto per la rifinitura.
Prima di ritagliare i singoli chip però, tutti i circuiti integrati devono essere testati per vedere se ce ne sono di alcuni non funzionanti (ce ne sono sempre): per eseguire il test i wafer vengono analizzati dai cosidetti 'wafer probers', ovvero speciali macchine che prendono i wafer, li allineano e creano i contatti per agganciarli ad una scheda di controllo.
Tutti i dice verranno scrupolosamente controllati tramite appositi (e solitamente proprietari) software, e quelli non funzionanti vengono marchiati, per essere poi scartati nella fase successiva.
Il rapporto tra dice prodotti e dice funzionanti e pronti per la vendita è chiamato resa, che di solito nelle grosse industrie di produzione (Intel e AMD su tutte) è molto alta: più del 90%.
Dopo il controllo, con unʼaltra costosissima macchina il wafer viene tagliato seguendo le linee dei suoi chip, che vengono separati.
Dicing è il nome del processo di taglio dei singoli chip, e viene fatto in automatico con la massima precisione.
I chip precedentemente marchiati perchè non funzionanti vengono a questo punto scartati.
Dopo il taglio, i singoli chip sono pronti per essere impacchettati in un contenitore di protezione, di solito di plastica o ceramica: è il package, e solitamente ha impresso sulla faccia superiore il logo dellʼindustria produttrice e il nome ed il numero di brevetto del microprocessore che contiene.

L'Intel Pentium (nome originario Intel 80586), la prima CPU iperscalare con due pipeline di dati
Lʼultima fase si chiama wire bonding e consiste nel saldare i fili di contatto dal chip ai pin del package, che verranno poi inseriti in una scheda madre di un calcolatore.
I grandi produttori mondiali di CPU
Nei primi microprocessori (compreso l'Intel 4004) i fili di contatto erano in oro puro, ma ora si utilizza lʼalluminio, o più recentemente il rame.
Come detto in precedenza, tutto questo processo di costruzione è lungo e richiede quasi due mesi di lavoro continuato.
Cʼè bisogno di attrezzature molto costose e dedicate, e tutto lʼambiente di lavoro deve essere in un clima di temperatura ottimale, in certe zone anche sottovuoto.
Ne consegue che una moderna fabbrica di CPU risulti dannatamente costosa, che per di più aumenta di costo nel tempo: nel 1995 infatti, unʼintera fabbrica completa veniva circa 700 milioni di dollari, mentre ora il prezzo è salito a circa 8 miliardi di dollari.
Per questo motivo al mondo solo pochissime industrie possono permettersi il lusso di produrre in proprio microprocessori, mentre la stragrande maggioranza dei produttori di apparecchiature che richiedono una qualsiasi CPU comperano le stesse da terze parti.
Ci sono praticamente tre grandi colossi nella produzione di CPU nel mondo, che soddisfano il mercato globale a circa il 90% (ed oltre).
In ordine di quote mercato i colossi sono:
- Intel
- AMD
- ARM
Fino alla fine degli anni 2000, la Motorola era una grande azienda che competeva più o meno alla pari con Intel ed AMD, poi discutibili scelte di mercato l'hanno portata ad una fine ingloriosa.
Parte della sua storica produzione sopravvive però nella Freescale Semiconductor, anche se la percentuale di mercato che ricopre l'azienda è risibile in confronto ad Intel e le altre.
I tre colossi producono circuiti integrati per le utenze più svariate, ma principalmente di natura consumer e scientifica.
Accanto alle industrie maggiori, in tutto il mondo (ed in particolare nel nord Italia) ci sono tante altre piccole industrie che invece producono sistemi integrati, solitamente embedded (ad esempio, la centrale elettronica di controllo che montano le autovetture recenti, o i lettori mp3, i router o dei telecomandi).
Il costo di produzione industriale delle CPU
Visto che il costo di produzione industriale non è dipeso dalla complessità di una CPU (anzi rimane invariato), tutti i produttori tentano sempre di progettare circuiti molto complessi e CPU molto potenti, per poi 'troncare' le potenzialità effettive delle stesse con limitatori hardware o software (per distinguerle in fasce di prezzo differenti).
Questo comportamento, da molti considerato scorretto, è comunque parte del sistema attuale di produzione industriale, e senza di esso una generica CPU di basse prestazioni verrebbe molto, molto più cara del prezzo attuale, visto che si dovrebbe progettare un circuito dedicato solo per essa.
Di rimando, le CPU vecchie sono comunque sempre prodotte e vendute, poichè sono appetibili commercialmente: grazie a layer già progettati, sperimentati e testati, vengono solo pochi centesimi al pezzo, che le rende utilissime per essere incorporate in dispositivi che non pretendono di comandare software particolarmente esosi di prestazioni.
Il parallelismo di calcolo
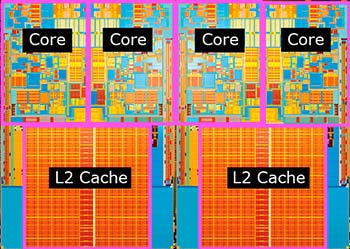
Una CPU con tecnologia Ivy Bridge dell'Intel, a quattro core di calcolo
Sul finire degli anni '90, la produzione delle CPU era quasi totalmente incentrata sul 'paradigma degli hertz', ovverosia della frequenza di clock: gli sforzi dei produttori erano rivolti principalmente ad aumentare i megahertz dei processori, per permettere più operazioni al secondo e, di rimando, più velocità di calcolo.
Questo assioma progettuale portò, anche grazie ad un marketing abbastanza selvaggio, ad avere processori con frequenze elevatissime (sfondando la soglia del gigahertz), ma che si portavano appresso pesanti problematiche delle loro vecchie architetture, mai del tutto risolte.
Oltre un certo valore di frequenza, i processori cominciavano a mostrare preoccupanti problemi di surriscaldamento, che fecero riconsiderare tutta la produzione a livello concettuale.
Il calcolo parallelo: esempio pratico
Per far capire la problematica con cui l'industria dei semiconduttori si trovò a combattere, è sufficiente fare un facile esempio: supponiamo che vi si chieda di contare da zero a dieci, nel più breve tempo possibile.
La velocità con la quale contate è comunque limitata dal fattore sequenziale: potete essere velocissimi nell'enunciare i numeri, ma comunque siete comunque obbligati a infilare i numeri uno dopo l'altro, senza possibilità di scorciatoie.
State quindi eseguendo un calcolo sequenziale, ovverosia calcolate singolarmente una data operazione, e solo quando quest'ultima è finita passate alla successiva.
Per contare più velocemente, avete in pratica solo un'opzione: velocizzare le singole operazioni, di modo che il tempo totale per la fine del calcolo s'accorci.
Discorso diverso è, invece, se tale operazione è effettuata da un gruppo di dieci persone, ognuna incaricata di contare solamente un numero: nello stesso momento, ognuna potrebbe contare uno ed un solo numero, facendo quindi finire la conta in 1/10 rispetto a quello che può fare una singola persona.
In molta sintesi, questo è il calcolo in parallelo: differenti unità ALU sincronizzate per risolvere la stessa problematica, aiutantosi a vicenda.
I sistemi multi-core
Per massimizzare le operazioni al secondo senza spingere troppo la frequenza di clock delle CPU, da metà anni 2000 il calcolo in parallelo cominciò ad essere introdotto come standard nell'industria dei semiconduttori anche per il mercato consumer.
Questa progettualità si rivelò vincente, e ben presto dai due processori fisici si arrivò a progettare e costruire due unità ALU costruite su un unico die, aprendo così la strada ai processori muli-core.
I risultati furono talmente apprezzabili che il calcolo in parallelo diventò il nuovo paradigma, prendendo il posto della frequenza pura e bruta tenuta in grande considerazione negli anni passati.
Ad oggi vengono prodotte CPU multi-core per qualsiasi esigenza, dai due sino ai sedici nuclei di calcolo ed oltre.
Tuttavia, il calcolo in parallelo servirebbe a poco (anzi, a niente) se non fosse supportato da software in grado di sfruttare il parallelismo: questo ha quindi richiesto molti anni di sforzi e duro lavoro da parte di programmatori e software house, per adattare o programmare ex novo programmi in grado di sfruttare i grandi vantaggi di più core di calcolo in simultanea.
I 'System-on-a-Chip'

Il SoC Apple A10 a 64 bit e quattro core di calcolo
Con l'avvento massiccio del mercato mobile verso la metà degli 2000, in particolar modo dell'ascesa degli smartphone e tablet, l'industria delle CPU si trovò di fronte ad una nuova sfida: produrre chip sufficientemente potenti ma possibilmente poco esosi di richieste energetiche, idonei ad essere saldati su schede logiche molto piccole, impossibilitate ad essere raffreddate con i sistemi canonici (ventole, in primis).
Fu così iniziata una lunga ricerca e sperimentazione da parte delle grandi major dei semiconduttori, con l'ARM in posizione privilegiata, in quanto già particolarmente attiva nel settore da qualche anno.
Questa ricerca, dettata dalla grande richiesta del mercato di sistemi mobili sempre più potenti, portò alla nascita di un particolare tipo di produzione iper-integrata, in cui CPU, GPU, RAM e controller principali è inclusa in un unico die (oppure, se ciò non è possibile, in un unico package).
Un circuito monoblocco in silicio in cui sono stati ricavate CPU, MMU e RAM, ovverosia gli elementi essenziali per un qualsiasi sistema, è per l'appunto chiamato "System-on-a-Chip" (abbreviato in SoC), e tale soluzione trova attualmente ampissimo utilizzo nel mercato degli smartphone e tablet, cominciandosi aprire anche al settore dei notebook e laptop.
Il mercato dei SoC ha conosciuto un'espansione senza precedenti in un lasso di tempo brevissimo: convenzionalmente, il mercato mobile degli smartphone si fa iniziare dalla presentazione del primo iPhone, svelato da Steve Jobs nel gennaio del 2007.
Uno dei primi a credere fortemente nelle potenzialita dei SoC, Jobs fece sviluppare dalla sua Apple il primo Apple A1, ovverosia un processore ARM a 620 Mhz (underclockato a 412 Mhz) con incluso un blocco RAM (eRAM, quindi embedded RAM) di 128 MB, a cui si integrava un chip grafico PowerVR MBX Lite 3D.
Una soluzione tecnica estremamente avanzata, uno dei primi esempi di successo commerciale di un SoC, che infatti fece la fortuna del nuovo cellulare prodotto da Apple, e a cui tutti gli altri produttori poi si aggregarono, in una competizione che, in circa 10 anni, portò un'evoluzione considerevole della tecnologia.
Allo stato attuale, vengono prodotti SoC a 64 bit con tecnologia multi-core per pressoché tutti gli smartphone ed i tablet esistenti, e la loro potenza d'elaborazione spesso eguaglia, quando no surclassa, i loro equivalenti per gli ambieti desktop.
La 'legge di Moore'

Gordon Moore, cofondatore dell'Intel e padre della legge che porta il suo nome
La complessità di un microcircuito, misurata tramite il numero di transistori per chip, raddoppia ogni 18 mesi.
Verso la metà degli anni '60, il cofondatore della Fairchild Semiconductor (e, sul finire del decennio, dell'Intel) Gordon Moore ipotizzò, basandosi su osservazioni prettamente empiriche, che il numero dei transistor in un dato circuito integrato potesse raddoppiare ogni 12 mesi.
Nel 1975, dopo l'inizio della rivoluzione iniziata da Faggin e a circa dieci anni dalla prima supposizione di Moore, il suo enunciato si dimostrò essenzialmente corretto, ma bisognò accomodare il tempo di raddoppio dei transistori a 24 mesi.
Tale lasso di tempo rimarrà veritiero per tutti gli anni '80, e sarà ritoccato solo sul finire degli anni '90, quando i mesi divennero 18.
Moore quindi fu tra i primi ad ipotizzare un successo massiccio della Very Large Scale Integration, e la sua legge è tutt'ora la base per i grandi produttori di CPU per valutare l'efficacia o meno della loro produzione di microprocessori.
Tuttavia, essendo basata su dati empirici, è una legge che molto probabilmente finirà di essere vera nel prossimo futuro: quando Moore ipotizzò la relazione tra numero di transistor e tempo, l'industria cominciava appena a progettare la produzione di massa di processori elettronici, in un'ottica concettuale profondamente differente da quella attuale.
Negli ultimi anni, più che il numero puro di transistor, a fare la differenza è stata la nuova architettura utilizzata, con l'introduzione del calcolo in parallello: la legge di Moore quindi dovrebbe essere considerata solo come una traccia, e ben altri fattori dovrebbero essere presi in esame per valutare la potenza di calcolo di una CPU.
Il costo di una fabbrica di chip raddoppia da una generazione all'altra.
La 'seconda legge di Moore'
La prima legge di Moore non è tuttavia la sola riflessione empirica che il produttore americano, padre dell'Intel, ci ha lasciato.
Esiste anche la cosidetta 'seconda legge di Moore' che, in estrema sintesi, analizza il costo industriale per produrre i chip.
Già nei primi anni '70, uno dei primi storici soci di Intel, l'imprenditore Arthur Rock, s'accorse con preoccupazione che il costo dei macchinari per produrre i chip praticamente raddoppiava ogni quattro anni, rendendo quindi l'investimento estremamente oneroso nel lungo periodo.
Moore ci ragionò un po' su, e negli anni '90 dai quattro anni stimati originariamente arrivò a dichiarare che il costo di un'intera fabbrica di microprocessori raddoppia da una generazione (di chip, ovviamente) all'altra.
Questo spiega gli enormi investimenti che Intel, AMD e le altre case costruttrici devono sostenere periodicamente e che comporta costi iniziali di vendita dei microprocessori decisamente elevati.
D'altra parte però, è doveroso notare come il costo di un singolo chip si dimezzi esponenzialmente col tempo trascorso dall'inizio della sua produzione: la seconda legge di Moore genera quindi un corollario, estremamente importante perché indica il costo di vendita di chip delle generazioni passate, non più così potenti da essere impiegati nella produzione digitale attuale ma essenziali per essere integrati nei sistemi embedded.
Se il telecomando di una generica TV moderna, di un apricancello, di un antifurto costa una cifra contenuta è perché la CPU che li regola ha raggiunto, nel tempo, un costo di pochi centesimi a pezzo.